Toán học

Hi guys! Gumawa ako ng 100-item Engineering Board Exam Questions for Mathematics na pwede nyong sagutan good for 4 hours as preboard exam na rin to test kung papasa kayo sa Math. 70 passing score.

Narito ang links ng videos ko for Engineering Board Exam Reviewers kung saan makikita nyo rin ang solutions sa exam. Please like and follow nyo na rin ang fb page natin na enginerdmath for more study and review materials. Good luck amd God bless future engineers!

ENGINEERING BOARD EXAM REVIEWERS PLAYLISTS

https://www.youtube.com/playlist...

https://youtu.be/Nx_4YOMuujw. - Algebra 1 Part 1

https://youtu.be/R5exSdU2uUM. -Algebra 1 Part 2

https://youtu.be/Ewd-z5tMwy8 -Algebra 2 Part 1

https://youtu.be/eO55JUAu9Bo -Algebra 2 Part 2

https://youtu.be/InsL-W28JT8. -Algebra 3 Part 1

https://youtu.be/SDpuPhb_pkk. - Algebra 3 Part 2

https://youtu.be/61S0IXeTmZE. - Algebra 4 Part 1

https://youtu.be/eXRtnHXh_70. - Algebra 4 Part 2

https://youtu.be/zvHpjiCwMxQ -Math Refresher Part 1

https://youtu.be/RsT6Gs45eMw - Calculus Part 1

https://youtu.be/x1A0WM9kKoQ - Probability and Statistics

https://youtu.be/dp5XWvNzsPQ - Math Refresher Part 2

https://youtu.be/gT1ipIaAs9k - Trigonometry Part 1

https://youtu.be/KJyrN8GorRk - Calculus Part 2

https://youtu.be/sb9h2TEbI2w- Plane and Solid Geometry Part 1

https://youtu.be/WYQf8uX1nNc- Differential Equations Part 1

https://youtu.be/J0fUHPSknzg- Math Refresher Part 3

https://www.youtube.com/channel/UCckZq2Y0Bfpha4D0CGG4W1g -Math Refresher Part 4

https://youtu.be/PovJJM71iUo - Calculator Techniques Part 1 (Algebra 1)

https://youtu.be/4EMV1ofGGZ4 - Calculator Techniques Part 2 (Algebra 2)

https://youtu.be/r4TUrT5LXG8 - Calculator Techniques Part 3 (Algebraic Equations)

https://youtu.be/Gpss4krXMT0 - Calculator Techniques Part 4 (First and Partial Derivatives)

https://youtu.be/ff4OmcVTQDc -Calculator Techniques Part 5 (Second Derivatives)

https://youtu.be/sMpp0p7meqo - Calculator Techniques Part 6 (Third Derivatives)

https://youtu.be/26z-t9NoErA -Calculator Techniques Part 7(Implicit Differentiation)

https://youtu.be/iLYaM_PS7H0 -Calculator Techniques Part 8 (Indefinite Integral)

https://youtu.be/CiheSw0ZLjk -Calculator Techniques Part 9 (Definite Integral)

https://youtu.be/eefcan5aq_U -Calculator Techniques Part 10( Differential Equations)

https://youtu.be/4l3MDRXiFEA -Calculator Techniques Part 11 (Solving First Order DE)

https://youtu.be/V8TbMh9Mp1g -Calculator Techniques Part 12(Solving Higher Order DE)

https://youtu.be/f-GnZD_Lj6s -Calculator Techniques Part 13(Areas Bounded by Curves)

https://youtu.be/pfdXMYXFhK0 -Calculator Techniques Part 14(Sequences and Series)

https://youtu.be/08ANEVyQsjg -Calculator Techniques Part 15(Arithmetic Sequence)

https://youtu.be/NdRqWWzITwA -Calculator Techniques Part 16 (Geometric Sequence)

https://youtu.be/_H0dJg6vTB8 -Calculator Techniques Part 17 (Laplace Transform)

https://youtu.be/fXOLQzRKygY -Calculator Techniques Part 18 (Inverse Laplace Transform)

https://youtu.be/xVerHU40KQc -Calculator Techniques Part 19 (Complex Numbers 1)

https://youtu.be/njvh56nXEPY -Calculator Techniques Part 20 (Complex Numbers 2)

https://youtu.be/iqWJL7dFIEM -Calculator Techniques Part 21 (Matrices)

https://youtu.be/oWQ6bhZRSTE -Calculator Techniques Part 22 (4X4 Determinants)

https://youtu.be/WtVBWNerxQA -Calculator Techniques Part 23 (5x5 Determinants)

https://youtu.be/sPwLNV4Rmi8 -Calculator Techniques Part 24 (Clock Problems)

https://youtu.be/e7CypitoYk4 -Calculator Techniques Part 25 (Angle Conversion)

https://youtu.be/-d0rMaWSQ-E -Calculator Techniques Part 26 (Trigo Identities/Equations)

https://youtu.be/5-bJ_xzJk4Y -Calculator Techniques Part 27 (Sine and Cosine Law)

https://youtu.be/sMpwjXzlOr0 -Calculator Techniques Part 28 (Functions)

https://youtu.be/qYmUhx6GJyA -Calculator Techniques Part 29 (Limits of Functions)

https://youtu.be/VTqujrqTPS4 -Calculator Techniques Part 30 (Maxima/Minima)

https://youtu.be/sGiPadRDFZQ -Math Refresher Part 6

https://youtu.be/7m_TUmavINQ -Math Refresher Part 7

https://youtu.be/di1yalzXwbI -Math Refresher Part 8

https://youtu.be/AeW8Iwsf0ag -Math Refresher Part 9

https://youtu.be/lz-JbXrbJmk -Math Refresher Part 10

https://youtu.be/Ocwpuz51Ojk -Math Refresher LS Part 1

https://youtu.be/IwDhCcDUlfc -Math Refresher LS Part 2

https://youtu.be/Kz-dKF7lMx8 -Math Refresher LS Part 3

https://youtu.be/NNzJ-haLQ_Q -Math Refresher LS Part 4

https://youtu.be/y5KlEMj-Zc8 -Math Refresher LS Part 5

https://youtu.be/gi_j-VTgPp0 -Math Refresher LS Part 6

https://youtu.be/wNIhm3sjPHg -Math Refresher LS Part 7

https://youtu.be/zF7AWXYEqGg -Math Refresher LS Part 8

https://youtu.be/IJEIdecST7k -Math Refresher LS Part 9

https://youtu.be/5O-8LREBk40 -Math Refresher LS Part 10

https://youtu.be/VBSfZm4HipI -Math Refresher LS Part 11

https://youtu.be/js2-MIyPuwM -Math Refresher LS Part 12

https://youtu.be/FvDcMKHbOfQ -Math Refresher LS Part 13

https://youtu.be/oWiVspDs300 -Math Refresher LS Part 14

https://youtu.be/M6OAN_qJ4GA -Math Refresher LS Part 15

https://youtu.be/DWrMOP1Qb8Y -Math Refresher LS Part 16

https://youtu.be/JzY77wYE8-4 -Math Refresher LS Part 17

GENERAL ENGINEERING &APPLIED SCIENCE (GEAS/ESAS)

https://www.youtube.com/playlist...

https://youtu.be/GHsSVfiaFu8 -Chemistry Part 1

https://youtu.be/sHeg_DK2hZ8 -Chemistry Part 2

https://youtu.be/EGjgUVrgBuU -Physics Part 1

https://youtu.be/zmRIMRzm4tA -Physics Part 2

https://youtu.be/l_BnbXfaPek -Engineering Mechanics Statics

https://youtu.be/TK8gDBpv9EY -Engineering Mechanics Dynamics

https://youtu.be/CkAp0jAEIa4 - General Engineering And Applied Science (GEAS/ESAS) Refresher Part 1

https://youtu.be/190hsMzoLUE - General Engineering And Applied Science (GEAS/ESAS) Refresher Part 2

ELECTRONICS REVIEWERS PLAYLIST

https://www.youtube.com/playlist...

ELECTRONIC SYSTEMS & TECHNOLOGY (EST)

https://www.youtube.com/playlist...

Please support me on YT by joining and get these perks:

JOIN: https://www.youtube.com/cha.../UCckZq2Y0Bfpha4D0CGG4W1g/join

https://youtu.be/THu7upJ8dfg

BENEFITS:

~You'll get a top fan badge on your name when you comment on my video.

~You'll have exclusive access to more supplemental math, science and engineering videos like reviewers, solved exam, etc. i personally make for Board Exam, CETs, CSE

~You'll have exclusive access to community post about math, science and engineering reviewers, notes, problem sets, in pdf forms, etc. i personally make which updates every week as good guide with your studies to pass your exams and subjects

~You’ll help me keep on making educational contents for free education in our country through my online videos

PDF file download link:

https://drive.google.com/.../1pI.../view...

Aside from this, you can also have access to may other math science and engineering notes which updates every week.

#enginerdmath

#educreator

#spreadtheloveformathscienceandengineering

𝐏𝐡𝐚̂𝐧 𝐭𝐢́𝐜𝐡 𝐲́ 𝐧𝐠𝐡𝐢̃𝐚 𝐜𝐨𝐞𝐟𝐟𝐢𝐜𝐢𝐞𝐧𝐭 𝐜𝐮̉𝐚 𝐥𝐨𝐠-𝐫𝐞𝐠 𝐯𝐚̀ 𝐧𝐨́ 𝐤𝐡𝐚́𝐜 𝐯𝐨̛́𝐢 𝐥𝐢𝐧𝐞𝐚𝐫-𝐫𝐞𝐠 𝐧𝐡𝐮̛ 𝐭𝐡𝐞̂́ 𝐧𝐚̀𝐨?

1. 𝑯𝒆̣̂ 𝒔𝒐̂́ 𝒕𝒓𝒐𝒏𝒈 𝑳𝒐𝒈𝒊𝒔𝒕𝒊𝒄 𝑹𝒆𝒈𝒓𝒆𝒔𝒔𝒊𝒐𝒏 𝒍𝒂̀ 𝒈𝒊̀?

Trong Logistic Regression, mục tiêu là dự đoán xác suất của một sự kiện (ví dụ: có bệnh hay không). Mô hình thực hiện việc này thông qua hàm sigmoid, chuyển đổi tổng trọng số thành giá trị nằm trong khoảng từ 0 đến 1. Công thức tổng quát được biểu diễn dưới dạng:

logit(p) = log(p/(1-p)) = beta0 + beta1 * x

Trong đó:

- p là xác suất dự đoán,

- beta0 là hệ số chặn (intercept),

- beta1 là hệ số (coefficient) của biến x.

Ý nghĩa của beta1:

- Nếu beta1 > 0: Khi biến x tăng 1 đơn vị, log-odds (tỉ số log của xác suất xảy ra sự kiện so với không xảy ra) tăng, tức là tỷ lệ odds (p/(1-p)) cũng tăng và từ đó xác suất p tăng.

- Nếu beta1 < 0: Khi x tăng 1 đơn vị, log-odds giảm, odds giảm và xác suất p giảm.

Để diễn giải trực quan hơn, ta có thể chuyển beta1 thành dạng tỷ lệ odds bằng cách tính exp(beta1). Ví dụ, nếu beta1 = 0.69 thì exp(0.69) khoảng 2, nghĩa là odds tăng gấp đôi khi biến x tăng 1 đơn vị.

2. 𝑯𝒆̣̂ 𝒔𝒐̂́ 𝒕𝒓𝒐𝒏𝒈 𝑳𝒊𝒏𝒆𝒂𝒓 𝑹𝒆𝒈𝒓𝒆𝒔𝒔𝒊𝒐𝒏 𝒍𝒂̀ 𝒈𝒊̀?

Trong Linear Regression, mô hình dự đoán giá trị liên tục (như giá nhà, nhiệt độ, v.v...) thông qua một phương trình tuyến tính đơn giản:

y_hat = w0 + w1 * x

Ở đây:

- w0 là intercept,

- w1 là hệ số của biến x.

Ý nghĩa của w1:

- Khi x tăng 1 đơn vị, giá trị dự đoán y_hat tăng thêm đúng w1 (nếu w1 dương) hoặc giảm (nếu w1 âm).

- Mối quan hệ giữa x và y_hat là sự thay đổi trực tiếp và tuyến tính, không liên quan đến xác suất hay odds như trong Logistic Regression.

3. 𝑺𝒖̛̣ 𝒌𝒉𝒂́𝒄 𝒃𝒊𝒆̣̂𝒕 𝒄𝒉𝒊́𝒏𝒉 𝒈𝒊𝒖̛̃𝒂 𝑳𝒐𝒈𝒊𝒔𝒕𝒊𝒄 𝑹𝒆𝒈𝒓𝒆𝒔𝒔𝒊𝒐𝒏 𝒗𝒂̀ 𝑳𝒊𝒏𝒆𝒂𝒓 𝑹𝒆𝒈𝒓𝒆𝒔𝒔𝒊𝒐𝒏

Một số điểm khác biệt quan trọng giữa hai mô hình này bao gồm:

𝑩𝒂̉𝒏 𝒄𝒉𝒂̂́𝒕 đ𝒂̂̀𝒖 𝒓𝒂:

𝘓𝘪𝘯𝘦𝘢𝘳 𝘙𝘦𝘨𝘳𝘦𝘴𝘴𝘪𝘰𝘯: Dự đoán giá trị thực, không giới hạn (có thể âm, dương).

𝘓𝘰𝘨𝘪𝘴𝘵𝘪𝘤 𝘙𝘦𝘨𝘳𝘦𝘴𝘴𝘪𝘰𝘯: Dự đoán xác suất, giá trị luôn nằm trong khoảng từ 0 đến 1.

𝒀́ 𝒏𝒈𝒉𝒊̃𝒂 𝒄𝒖̉𝒂 𝒉𝒆̣̂ 𝒔𝒐̂́:

𝘓𝘪𝘯𝘦𝘢𝘳 𝘙𝘦𝘨𝘳𝘦𝘴𝘴𝘪𝘰𝘯: Hệ số cho biết khi x tăng 1 đơn vị, giá trị y_hat thay đổi trực tiếp thêm w1.

𝘓𝘰𝘨𝘪𝘴𝘵𝘪𝘤 𝘙𝘦𝘨𝘳𝘦𝘴𝘴𝘪𝘰𝘯: Hệ số cho biết khi x tăng 1 đơn vị, log-odds thay đổi tương ứng; sau đó, ta có thể chuyển thành tỷ lệ odds bằng cách lấy exp(beta1) để hiểu mức độ tác động.

𝑷𝒉𝒖̛𝒐̛𝒏𝒈 𝒑𝒉𝒂́𝒑 𝒖̛𝒐̛́𝒄 𝒍𝒖̛𝒐̛̣𝒏𝒈:

𝘓𝘪𝘯𝘦𝘢𝘳 𝘙𝘦𝘨𝘳𝘦𝘴𝘴𝘪𝘰𝘯: Sử dụng phương pháp bình phương tối thiểu (Least Squares) để tối ưu.

𝘓𝘰𝘨𝘪𝘴𝘵𝘪𝘤 𝘙𝘦𝘨𝘳𝘦𝘴𝘴𝘪𝘰𝘯: Sử dụng Maximum Likelihood Estimation (MLE) do hàm sigmoid không phù hợp với cách giải tích như trong Linear Regression.

Nhờ những khác biệt này, các hệ số trong Logistic Regression được diễn giải dưới dạng tỷ lệ odds, giúp chúng ta hiểu rõ hơn mức độ ảnh hưởng của từng biến đầu vào lên xác suất xảy ra một sự kiện.

𝗖𝗮́𝗰 𝗯𝗶𝗲̂𝗻 𝘁𝗵𝗲̂̉ 𝗽𝗵𝗼̂̉ 𝗯𝗶𝗲̂́𝗻 𝗰𝘂̉𝗮 𝗡𝗮𝗶𝘃𝗲 𝗕𝗮𝘆𝗲𝘀 𝘃𝗮̀ 𝘀𝘂̛̣ 𝗸𝗵𝗮́𝗰 𝗻𝗵𝗮𝘂 𝗴𝗶𝘂̛̃𝗮 𝗰𝗵𝘂́𝗻𝗴

Naïve Bayes là một nhóm thuật toán phân loại dựa trên Định lý Bayes, giả định rằng các đặc trưng (features) độc lập với nhau, tức là giả định điều kiện độc lập (Naive assumption).

1. 𝑮𝒂𝒖𝒔𝒔𝒊𝒂𝒏 𝑵𝒂𝒊𝒗𝒆 𝑩𝒂𝒚𝒆𝒔 (𝑮𝑵𝑩)

Dùng khi nào? Khi dữ liệu là liên tục (continuous), ví dụ như chiều cao, cân nặng, điểm số, giá trị pixel của ảnh.

Giả sử các đặc trưng tuân theo phân phối chuẩn (Gaussian distribution) và tính xác suất bằng công thức: (trong ảnh 1)

𝟮. 𝗠𝘂𝗹𝘁𝗶𝗻𝗼𝗺𝗶𝗮𝗹 𝗡𝗮𝗶𝘃𝗲 𝗕𝗮𝘆𝗲𝘀 (𝗠𝗡𝗕)

Khuyên dùng khi dữ liệu là rời rạc và có số lần xuất hiện, phổ biến trong bài toán xử lý ngôn ngữ tự nhiên (NLP).

Cách hoạt động: Tính xác suất của một từ xuất hiện trong một lớp bằng công thức: (trong ảnh 3)

Ví dụ thực tế: Phân loại văn bản (spam detection, sentiment analysis), Phân loại tài liệu theo chủ đề.

3. 𝑩𝒆𝒓𝒏𝒐𝒖𝒍𝒍𝒊 𝑵𝒂𝒊𝒗𝒆 𝑩𝒂𝒚𝒆𝒔 (𝑩𝑵𝑩)

Khi dữ liệu là nhị phân (0/1), tức là mỗi đặc trưng chỉ có hai trạng thái (có hoặc không có) thì ta sẽ dùng BNB.

Mô hình giả định rằng một từ xuất hiện hay không xuất hiện trong tài liệu là quan trọng, thay vì số lần xuất hiện.

Công thức tính xác suất: (trong ảnh 2)

Ví dụ thực tế: Phân loại email spam (email chứa hoặc không chứa một số từ khóa spam), dự đoán một người có mắc bệnh dựa trên một số triệu chứng (có hoặc không có triệu chứng đó).

𝗞𝗲̂́𝘁 𝗹𝘂𝗮̣̂𝗻

- Gaussian Naïve Bayes phù hợp với dữ liệu liên tục.

- Multinomial Naïve Bayes phù hợp với dữ liệu rời rạc có số lần xuất hiện, thường dùng trong NLP.

- Bernoulli Naïve Bayes phù hợp với dữ liệu nhị phân, chỉ quan tâm đến sự xuất hiện hay không của đặc trưng.

Việc chọn loại Naive Bayes phù hợp tùy thuộc vào kiểu dữ liệu của bạn.

Like

Comment

Share

𝗟𝗼𝗴𝗶𝘀𝘁𝗶𝗰 𝗥𝗲𝗴𝗿𝗲𝘀𝘀𝗶𝗼𝗻 – 𝗧𝘂𝘆𝗲̂́𝗻 𝘁𝗶́𝗻𝗵 𝗵𝗮𝘆 𝗽𝗵𝗶 𝘁𝘂𝘆𝗲̂́𝗻 𝘁𝗶́𝗻𝗵?

Nếu bạn mới học Machine Learning, có thể bạn sẽ thắc mắc: Logistic Regression có phải là một mô hình tuyến tính không? Vì đầu ra của nó là một xác suất (trong khoảng [0,1]), nhiều người nghĩ rằng nó là một mô hình phi tuyến tính. Nhưng sự thật là, Logistic Regression vẫn là một mô hình tuyến tính!

𝗕𝗮̉𝗻 𝗰𝗵𝗮̂́𝘁 𝘁𝘂𝘆𝗲̂́𝗻 𝘁𝗶́𝗻𝗵 𝗰𝘂̉𝗮 𝗟𝗼𝗴𝗶𝘀𝘁𝗶𝗰 𝗥𝗲𝗴𝗿𝗲𝘀𝘀𝗶𝗼𝗻

Trước tiên, hãy cùng nhìn vào công thức của Logistic Regression:

z=w1x1+w2x2+...+wnxn+bz

Đây chính là một tổ hợp tuyến tính của các biến đầu vào X. Tuy nhiên, thay vì dự đoán trực tiếp z, mô hình sử dụng hàm sigmoid để chuyển đổi nó thành một xác suất: (Trong ảnh)

Hàm sigmoid giúp đảm bảo rằng đầu ra luôn nằm trong khoảng [0,1], phù hợp với bài toán phân loại nhị phân (binary classification)

𝗩𝗮̣̂𝘆 𝗟𝗼𝗴𝗶𝘀𝘁𝗶𝗰 𝗥𝗲𝗴𝗿𝗲𝘀𝘀𝗶𝗼𝗻 𝗰𝗼́ 𝗽𝗵𝗶 𝘁𝘂𝘆𝗲̂́𝗻 𝘁𝗶́𝗻𝗵 𝗸𝗵𝗼̂𝗻𝗴?

Câu trả lời là KHÔNG. Mặc dù đầu ra cuối cùng không phải là một kết hợp tuyến tính của X, nhưng mô hình vẫn được coi là tuyến tính trên log-odds space.

Tại sao? Vì nếu ta lấy logit function của xác suất p, ta thu được một phương trình tuyến tính: (Trong hình có cách biến đổi log-odds)

Logit function giúp biến đổi xác suất về khoảng (−∞,+∞) biến mô hình trở thành một linear model trong không gian log-odds.

𝗧𝗮̣𝗶 𝘀𝗮𝗼 𝗹𝗮̣𝗶 𝗾𝘂𝗮𝗻 𝘁𝗿𝗼̣𝗻𝗴?

Hiểu được Logistic Regression là một mô hình tuyến tính giúp chúng ta biết được những giới hạn của nó:

Ưu điểm:

- Dễ huấn luyện, nhanh chóng và hiệu quả trên các tập dữ liệu nhỏ.

- Có thể giải thích được (interpretability) vì mỗi hệ số wi​ cho thấy mức độ ảnh hưởng của từng biến đến log-odds.

- Không yêu cầu quá nhiều dữ liệu để hoạt động tốt.

Nhược điểm:

- Vì bản chất tuyến tính, Logistic Regression không thể nắm bắt các mối quan hệ phi tuyến giữa biến đầu vào và đầu ra.

- Nếu dữ liệu không tách biệt tuyến tính, Logistic Regression có thể hoạt động kém.

Nếu muốn xử lý các bài toán có quan hệ phi tuyến giữa biến đầu vào và đầu ra, ta cần biến đổi đặc trưng (Feature Engineering) hoặc dùng các mô hình phức tạp hơn như Decision Trees, Random Forest, hay Neural Networks.

𝐑-𝐬𝐪𝐮𝐚𝐫𝐞𝐝 𝐯𝐚̀ 𝐀𝐝𝐣𝐮𝐬𝐭𝐞𝐝 𝐑-𝐬𝐪𝐮𝐚𝐫𝐞𝐝

𝐑-𝐬𝐪𝐮𝐚𝐫𝐞𝐝 𝐯𝐚̀ 𝐀𝐝𝐣𝐮𝐬𝐭𝐞𝐝 𝐑-𝐬𝐪𝐮𝐚𝐫𝐞𝐝

R-squared (R2) và Adjusted R-squared (Radj2) đều là các chỉ số quan trọng trong hồi quy tuyến tính, giúp đánh giá mức độ phù hợp của mô hình với dữ liệu. R-squared đo lường tỷ lệ phương sai của biến phụ thuộc được giải thích bởi các biến độc lập. Chỉ số này càng cao thì mô hình càng phù hợp với dữ liệu. Tuy nhiên, nhược điểm của R-squared là nó luôn tăng khi thêm biến độc lập vào mô hình, ngay cả khi biến đó không thực sự có ý nghĩa thống kê, dẫn đến nguy cơ overfitting.

Để khắc phục vấn đề này, Adjusted R-squared được sử dụng nhằm điều chỉnh giá trị R-squared bằng cách tính đến số lượng biến độc lập trong mô hình. Khác với R-squared, Adjusted R-squared chỉ tăng khi biến mới thực sự cải thiện mô hình và sẽ giảm nếu biến đó không có ý nghĩa.

Trong công thức của Adjusted R-squared sẽ bổ sung thêm 2 thành phần là

Trong đó:

- N Số lượng quan sát (sample size)

- p Số lượng biến độc lập

𝑲𝒉𝒊 𝒏𝒂̀𝒐 𝒕𝒂 𝒏𝒆̂𝒏 𝒔𝒖̛̉ 𝒅𝒖̣𝒏𝒈 𝑨𝒅𝒋𝒖𝒔𝒕𝒆𝒅 𝑹-𝒔𝒒𝒖𝒂𝒓𝒆𝒅?

- Khi có nhiều biến độc lập và cần kiểm tra xem biến nào thực sự quan trọng

- Khi so sánh nhiều mô hình hồi quy có số lượng biến khác nhau

- Khi muốn tránh overfitting do thêm biến không cần thiết

𝗩𝗶́ 𝗱𝘂̣ 𝘁𝗵𝘂̛̣𝗰 𝘁𝗲̂́: Bạn đang xây dựng mô hình dự đoán giá nhà với 10 biến độc lập. Nếu bạn thêm một biến mới (số lượng bãi đậu xe trong khu vực), R2 có thể tăng nhẹ nhưng biến này có thể không có ý nghĩa thực tế. Radj2 sẽ giúp kiểm tra xem biến này có thực sự cải thiện mô hình hay không.

𝗛𝗶𝗲̂̉𝘂 𝘃𝗲̂̀ 𝗴𝗶𝗮̉ đ𝗶̣𝗻𝗵 𝘁𝘂𝘆𝗲̂́𝗻 𝘁𝗶́𝗻𝗵 𝘁𝗿𝗼𝗻𝗴 𝗵𝗼̂̀𝗶 𝗾𝘂𝘆 𝘁𝘂𝘆𝗲̂́𝗻 𝘁𝗶́𝗻𝗵

Giả định về tính tuyến tính là một trong những nền tảng quan trọng giúp mô hình hồi quy tuyến tính hoạt động chính xác. Nhưng liệu bạn đã thực sự hiểu rõ vai trò, cách kiểm tra và xử lý khi giả định này bị vi phạm chưa? Hãy cùng phân tích chi tiết nhé!

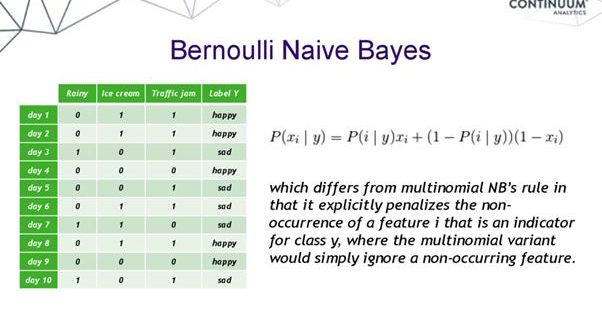
Hồi quy tuyến tính giả định rằng mối quan hệ giữa biến độc lập (X) và biến phụ thuộc là tuyến tính. Công thức cơ bản của mô hình như sau:

𝗬=β𝟬+β𝟭𝗫𝟭+β𝟮𝗫𝟮+...+β𝗻𝗫𝗻+ϵ

Trong đó:

- β0​: Hệ số chặn (intercept).

- β1,β2,...,βn​: Các hệ số góc đại diện cho mức độ ảnh hưởng của các biến độc lập X1,X2,...,Xn

- ϵ: Sai số ngẫu nhiên.

Hồi quy tuyến tính dựa trên giả định rằng mối quan hệ giữa các biến là tuyến tính. Nếu giả định này không được đáp ứng, các hệ số β sẽ bị sai lệch, dẫn đến kết quả dự đoán không chính xác.

𝙂𝙞𝙖̉𝙞 𝙩𝙝𝙞́𝙘𝙝 𝙫𝙚̂̀ 𝙢𝙖̣̆𝙩 𝙮́ 𝙣𝙜𝙝𝙞̃𝙖 𝙩𝙝𝙤̂́𝙣𝙜 𝙠𝙚̂: Mối quan hệ tuyến tính giúp chúng ta hiểu rõ mức độ ảnh hưởng của từng biến X lên Y. Nếu mối quan hệ không tuyến tính, các hệ số hồi quy sẽ mất ý nghĩa.

Ngoài ra, chúng ta còn phân tích sự phụ thuộc giữa các biến độc lập X nữa hay còn gọi là đ𝗮 𝗰𝗼̣̂𝗻𝗴 𝘁𝘂𝘆𝗲̂́𝗻 (𝗺𝘂𝗹𝘁𝗶𝗰𝗼𝗹𝗹𝗶𝗻𝗲𝗮𝗿𝗶𝘁𝘆).Nếu Xi và Xj có mối quan hệ tuyến tính cao, mô hình sẽ khó xác định tác động độc lập của từng biến lên biến phụ thuộc .

Vì vậy trước khi thực hiện quá trình training với tập dữ liệu có n biến X thì số lần chúng ta cần thực hiện kiểm tra mối quan hệ là: 2Cn (từng cặp X) + n (từng Xi với Y)

𝗖𝗮́𝗰𝗵 𝗸𝗶𝗲̂̉𝗺 𝘁𝗿𝗮 𝗴𝗶𝗮̉ đ𝗶̣𝗻𝗵 𝘃𝗲̂̀ 𝘁𝗶́𝗻𝗵 𝘁𝘂𝘆𝗲̂́𝗻 𝘁𝗶́𝗻𝗵

𝙃𝙚̣̂ 𝙨𝙤̂́ 𝙩𝙪̛𝙤̛𝙣𝙜 𝙦𝙪𝙖𝙣 (𝙘𝙤𝙧𝙧𝙚𝙡𝙖𝙩𝙞𝙤𝙣 𝙘𝙤𝙚𝙛𝙛𝙞𝙘𝙞𝙚𝙣𝙩): nhưng cần lưu ý rằng đây chỉ là một phương pháp sơ bộ (Nó theo hình thức lý thuyết xác suất - thống kê thôi). Để kiểm tra sâu hơn về giả định tuyến tính, ngoài việc dùng hệ số tương quan, bạn nên kết hợp thêm các phương pháp bên dưới.

𝙑𝙚̃ 𝙗𝙞𝙚̂̉𝙪 đ𝙤̂̀ 𝙨𝙘𝙖𝙩𝙩𝙚𝙧 𝙥𝙡𝙤𝙩 𝙜𝙞𝙪̛̃𝙖 𝙩𝙪̛̀𝙣𝙜 𝙘𝙖̣̆𝙥: Nếu mối quan hệ là tuyến tính, bạn sẽ thấy các điểm phân bố theo một đường thẳng hoặc gần như đường thẳng.

𝙍𝙚𝙨𝙞𝙙𝙪𝙖𝙡 𝙋𝙡𝙤𝙩: Vẽ đồ thị phần dư (residuals) theo các giá trị dự đoán (predicted values). Nếu giả định tuyến tính đúng, các phần dư sẽ phân bố ngẫu nhiên xung quanh trục ngang (không có mẫu hình rõ ràng).

𝗚𝗶𝗮̉𝗶 𝗽𝗵𝗮́𝗽 𝗸𝗵𝗶 𝗴𝗶𝗮̉ đ𝗶̣𝗻𝗵 𝘁𝘂𝘆𝗲̂́𝗻 𝘁𝗶́𝗻𝗵 𝗯𝗶̣ 𝘃𝗶 𝗽𝗵𝗮̣𝗺

(Mình hay dùng cách 2)

𝗖𝗮́𝗰𝗵 𝟭: Biến đổi biến độc lập.

- Logarithm (log⁡(X))

- Căn bậc hai của X

- Đa thức (X^2,X^3) (Có lẽ trong bài tìm hiểu về SVM ta sẽ tìm hiểu phần này)

𝗖𝗮́𝗰𝗵 𝟮: Sử dụng mô hình phi tuyến.

- Random Forest hoặc Decision Tree.

- Neural Networks nếu dữ liệu lớn và phi tuyến tính rõ rệt.

Một bài demo dự đoán giá nhà mà mình thực hiện hồi quy tuyến tính nha

Link demo: https://colab.research.google.com/.../1AXCv...

𝗣𝗵𝗮̂𝗻 𝘁𝗶́𝗰𝗵 đ𝗮̣̆𝗰 𝘁𝗿𝘂̛𝗻𝗴 𝗰𝘂̉𝗮 𝗪 (𝘁𝗿𝗼̣𝗻𝗴 𝘀𝗼̂́) 𝘁𝗿𝗼𝗻𝗴 𝗹𝗼𝗴𝗶𝘀𝘁𝗶𝗰 𝗿𝗲𝗴𝗿𝗲𝘀𝘀𝗶𝗼𝗻

𝗣𝗵𝗮̂𝗻 𝘁𝗶́𝗰𝗵 đ𝗮̣̆𝗰 𝘁𝗿𝘂̛𝗻𝗴 𝗰𝘂̉𝗮 𝗪 (𝘁𝗿𝗼̣𝗻𝗴 𝘀𝗼̂́) 𝘁𝗿𝗼𝗻𝗴 𝗹𝗼𝗴𝗶𝘀𝘁𝗶𝗰 𝗿𝗲𝗴𝗿𝗲𝘀𝘀𝗶𝗼𝗻

Trong 𝗟𝗼𝗴𝗶𝘀𝘁𝗶𝗰 𝗥𝗲𝗴𝗿𝗲𝘀𝘀𝗶𝗼𝗻, trọng số W đóng vai trò cực kỳ quan trọng trong việc định hình hành vi của hàm sigmoid và cách mô hình phân loại dữ liệu bởi vì W đóng vai trò như một hệ số điều chỉnh độ dốc của đường cong 𝘀𝗶𝗴𝗺𝗼𝗶𝗱. Cùng phân tích tác động của W lên đường cong sigmoid nhé!

𝑪𝒐̂𝒏𝒈 𝒕𝒉𝒖̛́𝒄 𝒉𝒂̀𝒎 𝒔𝒊𝒈𝒎𝒐𝒊𝒅

Hàm sigmoid được định nghĩa là: hình bên dưới

Trong đó: g(z) = sigmoid(z) = sigmoid(wx + b)

- x: đầu vào.

- W: trọng số, điều chỉnh tốc độ thay đổi của g(x) theo x.

- b: là bias

Đ𝒂̣𝒐 𝒉𝒂̀𝒎 𝒗𝒂̀ đ𝒐̣̂ 𝒅𝒐̂́𝒄

Độ dốc của hàm sigmoid được xác định bởi đạo hàm của nó: h′(x)=h(x)⋅(1−h(x))⋅W

thì h′(x) đạt cực đại tại h(x)=0.5, nghĩa là tại x=0: h′(0)=W/4

𝑻𝑯1: 𝑲𝒉𝒊 𝑾>1: Đường cong trở nên sắc nét hơn (sharp)

Khi giá trị W càng lớn, đường cong sigmoid trở nên dốc hơn ở vùng trung tâm (gần ngưỡng 0.5). Mô hình đưa ra quyết định phân loại nhanh chóng hơn khi dữ liệu nằm gần ranh giới. Tuy nhiên, nếu W quá lớn, mô hình dễ bị overfitting.

𝑻𝑯2: 𝑲𝒉𝒊 0<𝑾<1: Đường cong mượt hơn (smooth)

Với W nhỏ hơn 1, đường cong sigmoid thay đổi từ từ (đường cong sẽ mịn hơn). Xác suất dự đoán biến đổi chậm, phù hợp với dữ liệu có sự phân tách không rõ ràng. Mô hình trở nên ổn định hơn, ít nhạy cảm với nhiễu.

𝑻𝑯3: 𝑲𝒉𝒊 𝑾<0: Đường cong bị đảo chiều

Khi W mang giá trị âm, đường cong sigmoid bị đảo ngược. Trọng số âm cho thấy thuộc tính này giảm xác suất thuộc lớp 1 khi giá trị tăng.

Ví dụ: Trong dự đoán sức khỏe, số giờ tập thể dục (với W<0) có thể giảm xác suất mắc bệnh.

𝙑𝙖̣̂𝙮 𝙣𝙚̂𝙣, 𝙫𝙞𝙚̣̂𝙘 𝙩𝙤̂́𝙞 𝙪̛𝙪 𝙩𝙧𝙤̣𝙣𝙜 𝙨𝙤̂́ 𝙒 𝙠𝙝𝙤̂𝙣𝙜 𝙘𝙝𝙞̉ 𝙜𝙞𝙪́𝙥 𝙢𝙤̂ 𝙝𝙞̀𝙣𝙝 𝙙𝙪̛̣ đ𝙤𝙖́𝙣 𝙘𝙝𝙞́𝙣𝙝 𝙭𝙖́𝙘 𝙢𝙖̀ 𝙘𝙤̀𝙣 𝙝𝙞𝙚̂̉𝙪 𝙧𝙤̃ đ𝙖̣̆𝙘 đ𝙞𝙚̂̉𝙢 𝙦𝙪𝙖𝙣 𝙩𝙧𝙤̣𝙣𝙜 𝙩𝙧𝙤𝙣𝙜 𝙙𝙪̛̃ 𝙡𝙞𝙚̣̂𝙪.

𝗧𝗮̣𝗶 𝘀𝗮𝗼 𝗴𝗼̣𝗶 𝗹𝗮̀ 𝗡𝗮𝗶𝘃𝗲 𝗕𝗮𝘆𝗲𝘀?

𝗡𝗮𝗶𝘃𝗲 𝗕𝗮𝘆𝗲𝘀 là một thuật toán học máy cực kỳ phổ biến trong phân loại, nhưng tại sao lại gọi là "naive" (ngây thơ)?

"Naive" ở đây là vì thuật toán này giả định rằng các đặc trưng (features) trong dữ liệu là độc lập với nhau khi biết lớp (label). Nghe đơn giản quá phải không?

Ví dụ, trong bài toán phân loại email spam, 𝗡𝗮𝗶𝘃𝗲 𝗕𝗮𝘆𝗲𝘀 sẽ giả định rằng từ "free" và "money" không liên quan đến nhau, dù thực tế chúng thường đi chung trong email rác. Nhưng thuật toán này vẫn cho kết quả rất tốt trong thực tế!

𝗚𝗶𝗮̉ đ𝗶̣𝗻𝗵 𝗰𝘂̉𝗮 𝗡𝗮𝗶𝘃𝗲 𝗕𝗮𝘆𝗲𝘀 𝗹𝗮̀ 𝗴𝗶̀?

Naive Bayes dựa trên một giả định gọi là 𝗖𝗼𝗻𝗱𝗶𝘁𝗶𝗼𝗻𝗮𝗹 𝗜𝗻𝗱𝗲𝗽𝗲𝗻𝗱𝗲𝗻𝗰𝗲 (Độc lập có điều kiện). Có nghĩa là:

Khi biết lớp (label), các đặc trưng không còn phụ thuộc vào nhau nữa.

𝘾𝙤̂𝙣𝙜 𝙩𝙝𝙪̛́𝙘: P(X1,X2,...,Xn∣Y) = P(X1​∣Y)⋅P(X2​∣Y)⋅...⋅ P(Xn​∣Y)

Điều này giúp thuật toán tính toán dễ dàng và nhanh chóng hơn rất nhiều, thay vì phải xử lý toàn bộ mối quan hệ giữa các đặc trưng.

Đ𝗼̣̂𝗰 𝗹𝗮̣̂𝗽 𝘃𝗮̀ 𝗽𝗵𝘂̣ 𝘁𝗵𝘂𝗼̣̂𝗰 𝗸𝗵𝗮́𝗰 𝗻𝗵𝗮𝘂 𝘁𝗵𝗲̂́ 𝗻𝗮̀𝗼?

𝙄𝙣𝙙𝙚𝙥𝙚𝙣𝙙𝙚𝙣𝙘𝙚 (Đ𝙤̣̂𝙘 𝙡𝙖̣̂𝙥)

Hai sự kiện A và B là độc lập nếu: P(A∩B)=P(A)⋅P(B)

Điều này có nghĩa là xác suất xảy ra của sự kiện A không bị ảnh hưởng bởi sự kiện B và ngược lại. Trong ngữ cảnh của Naive Bayes, tính độc lập giữa các đặc trưng có nghĩa là, nếu chúng ta biết lớp Y, sự thay đổi trong giá trị của một đặc trưng không ảnh hưởng đến xác suất của các đặc trưng còn lại.

Ví dụ: Trong một bài toán phân loại email spam, Naive Bayes giả định rằng các từ trong email là độc lập với nhau khi đã biết email là spam hay không. Thực tế, điều này có thể không chính xác (vì các từ có thể có mối quan hệ với nhau, ví dụ "free" và "money" thường xuất hiện cùng nhau trong email spam), nhưng giả định này vẫn hữu ích trong nhiều trường hợp.

𝗗𝗲𝗽𝗲𝗻𝗱𝗲𝗻𝗰𝗲 (𝗣𝗵𝘂̣ 𝘁𝗵𝘂𝗼̣̂𝗰)

Hai sự kiện A và B là phụ thuộc nếu: P(A∩B)≠P(A)⋅P(B)

Điều này có nghĩa là xác suất xảy ra của sự kiện A bị ảnh hưởng bởi sự kiện B và ngược lại. Trong các bài toán thực tế, các đặc trưng thường có sự phụ thuộc với nhau, ví dụ trong bài toán nhận diện khuôn mặt, các đặc trưng về ánh sáng và góc nhìn có thể có sự phụ thuộc nhất định.

Trong thực tế, các đặc trưng trong dữ liệu thường phụ thuộc lẫn nhau. Nhưng Naive Bayes vẫn giả định chúng độc lập để đơn giản hóa bài toán – đây chính là lý do nó được gọi là "ngây thơ"!

𝗞𝗲̂́𝘁 𝗹𝘂𝗮̣̂𝗻:

𝗡𝗮𝗶𝘃𝗲 𝗕𝗮𝘆𝗲𝘀 có thể "ngây thơ" trong giả định, nhưng nhờ sự đơn giản này mà nó trở nên cực kỳ hiệu quả và phổ biến, đặc biệt là trong các bài toán như:

- Phân loại văn bản (email spam, cảm xúc bình luận).

- Nhận diện ngôn ngữ.

Và nhiều ứng dụng khác.

Ngây thơ đôi khi lại là sức mạnh!

Bạn đã dùng Naive Bayes trong dự án nào chưa? Chia sẻ ở dưới nhé!

𝗘𝗻𝘁𝗿𝗼𝗽𝘆 - 𝗠𝘂̛́𝗰 đ𝗼̣̂ "𝗵𝗼̂̃𝗻 𝗹𝗼𝗮̣𝗻" 𝘁𝗿𝗼𝗻𝗴 𝗱𝘂̛̃ 𝗹𝗶𝗲̣̂𝘂!

𝗘𝗻𝘁𝗿𝗼𝗽𝘆 - 𝗠𝘂̛́𝗰 đ𝗼̣̂ "𝗵𝗼̂̃𝗻 𝗹𝗼𝗮̣𝗻" 𝘁𝗿𝗼𝗻𝗴 𝗱𝘂̛̃ 𝗹𝗶𝗲̣̂𝘂!

Nếu bạn đang học về học máy hoặc lý thuyết thông tin, chắc chắn bạn đã nghe đến thuật ngữ 𝗘𝗻𝘁𝗿𝗼𝗽𝘆. Nhưng bạn đã hiểu đúng về nó chưa? Hãy cùng tìm hiểu nhé!

𝗘𝗻𝘁𝗿𝗼𝗽𝘆 là gì? Đơn giản mà nói, 𝗘𝗻𝘁𝗿𝗼𝗽𝘆 là thước đo mức độ không chắc chắn hoặc hỗn loạn trong một tập dữ liệu. Khi bạn có một dữ liệu mà các lớp (classes) phân bố đều, nghĩa là có sự hỗn loạn lớn. Ngược lại, nếu dữ liệu thuộc cùng một lớp, 𝗘𝗻𝘁𝗿𝗼𝗽𝘆 sẽ rất thấp, tức là bạn đã có một dữ liệu rất "chắc chắn" và dễ hiểu.

Công thức đơn giản: (trong ảnh nha).

Ví dụ: (Trong ảnh luôn nha)

Decision Tree phân chia dữ liệu tại một nút, chúng ta tính toán 𝗘𝗻𝘁𝗿𝗼𝗽𝘆 cho mỗi nhóm con sau phân chia. Mục tiêu là chọn thuộc tính phân chia sao cho 𝗘𝗻𝘁𝗿𝗼𝗽𝘆 của các nhóm con càng thấp càng tốt. Khi 𝗘𝗻𝘁𝗿𝗼𝗽𝘆 giảm, tức là sự không chắc chắn về lớp của dữ liệu giảm, giúp cải thiện độ chính xác của mô hình.

Quá trình sử dụng 𝗘𝗻𝘁𝗿𝗼𝗽𝘆 trong Decision Tree:

- Tính 𝗘𝗻𝘁𝗿𝗼𝗽𝘆 cho tập dữ liệu gốc.

- Phân chia dữ liệu theo các thuộc tính và tính 𝗘𝗻𝘁𝗿𝗼𝗽𝘆 cho mỗi nhóm con.

- Chọn thuộc tính phân chia sao cho 𝗘𝗻𝘁𝗿𝗼𝗽𝘆 giảm nhiều nhất, tức là sự phân chia sẽ làm giảm độ không chắc chắn của dữ liệu.

- Lặp lại cho các nhóm con cho đến khi 𝗘𝗻𝘁𝗿𝗼𝗽𝘆 bằng 0 (hoàn toàn thuần nhất) hoặc đạt điều kiện dừng.

𝗥-𝘀𝗾𝘂𝗮𝗿𝗲𝗱

𝗛𝗶𝗲̂̉𝘂 𝗩𝗲̂̀ 𝗥-𝘀𝗾𝘂𝗮𝗿𝗲𝗱: 𝗖𝗵𝗶̉ 𝗦𝗼̂́ "𝗤𝘂𝘆𝗲̂̀𝗻 𝗟𝘂̛̣𝗰" 𝗧𝗿𝗼𝗻𝗴 𝗛𝗼̂̀𝗶 𝗤𝘂𝘆 𝗧𝘂𝘆𝗲̂́𝗻 𝗧𝗶́𝗻𝗵

Nếu bạn đang làm việc với các mô hình hồi quy tuyến tính hoặc đơn giản chỉ quan tâm đến cách mô hình "hiểu" dữ liệu, chắc hẳn bạn đã nghe qua về 𝗥-𝘀𝗾𝘂𝗮𝗿𝗲𝗱 (R2). Đây là một trong những chỉ số phổ biến nhất để đánh giá mức độ mà mô hình của bạn giải thích được biến thiên của dữ liệu. Nhưng... liệu bạn đã hiểu đúng về nó chưa?

𝗥-𝘀𝗾𝘂𝗮𝗿𝗲𝗱 𝗹𝗮̀ 𝗴𝗶̀?

Hiểu đơn giản, 𝗥-𝘀𝗾𝘂𝗮𝗿𝗲𝗱 trả lời câu hỏi: "Mô hình của bạn giải thích được bao nhiêu phần trăm biến động trong dữ liệu mục tiêu ?"

Công thức: (dưới hình ảnh nha)

Nghe phức tạp đúng không? Đừng lo, mình sẽ giải thích:

𝙏𝙤̂̉𝙣𝙜 𝙗𝙞𝙚̂́𝙣 𝙩𝙝𝙞𝙚̂𝙣 (𝙎𝙎𝙩𝙤𝙩​): Đây là tổng độ dao động của giá trị thực tế y so với giá trị trung bình của chúng (thể hiện độ biến thiên của dữ liệu thực tế xung quanh giá trị trung bình đó).

𝙋𝙝𝙖̂̀𝙣 𝙙𝙪̛ (𝙎𝙎𝙧𝙚𝙨𝙨): Đây là tổng sai số giữa giá trị thực tế y và giá trị mô hình dự đoán y’ ( Đây là "phần mô hình chưa giải thích được", hay nói cách khác là phần lỗi của mô hình.).

Nếu mô hình "lý tưởng", toàn bộ dao động của y đều được giải thích thì R2 sẽ bằng 1. Nhưng nếu mô hình kém, không giải thích được gì cả thì R2 = 0. Hiểu đơn giản hơn thì nó chính là phần trăm biến động của y mà mô hình có thể giải thích được.

Ví dụ thực tế

Bạn đang xây dựng một mô hình để dự đoán doanh thu cửa hàng dựa trên chi phí quảng cáo ở 3 kênh: TV, radio, và mạng xã hội.

𝑲𝒊̣𝒄𝒉 𝒃𝒂̉𝒏 1: R2=0.85 → Mô hình giải thích được 85% biến động trong doanh thu. Khá ổn đấy! Nhưng vẫn còn 15% dao động có thể do các yếu tố khác như chất lượng sản phẩm, đối thủ cạnh tranh,...

𝑲𝒊̣𝒄𝒉 𝒃𝒂̉𝒏 2: R2=0.45 → Mô hình chỉ giải thích được 45%. Bạn cần xem lại liệu dữ liệu quảng cáo có thực sự ảnh hưởng mạnh đến doanh thu không, hoặc có đang thiếu yếu tố quan trọng nào?

Đ𝗶𝗲̂̉𝗺 𝗺𝗮̂́𝘂 𝗰𝗵𝗼̂́𝘁

𝗥-𝘀𝗾𝘂𝗮𝗿𝗲𝗱 là chỉ số tuyệt vời để đánh giá độ phù hợp của mô hình. Tuy nhiên, nó không phản ánh độ chính xác của dự đoán, và không phải lúc nào R2 cao cũng là tốt. Hãy luôn kết hợp với các chỉ số khác như MSE, RMSE hoặc MAE để có cái nhìn toàn diện hơn.

Bạn xây dựng mô hình hồi quy để dự đoán doanh thu của một cửa hàng dựa trên số lượng quảng cáo, nhưng dữ liệu doanh thu bị nhiễu lớn (do các yếu tố khác như thời tiết, kinh tế, v.v.). Mô hình tuyến tính có thể đạt R² cao (ví dụ: 0.90) nhưng sai số dự đoán vẫn lớn (RMSE hoặc MAE cao). Hoặc trường hợp mô hình bị overfitting và R2 nó cũng sẽ khá cao nữa.

Bạn đã từng gặp trường hợp R2 "lừa dối" mình chưa? Chia sẻ bên dưới nhé!

Quantum Mechanics: Dirac's Equation

 

Mạng nơ-ron tích chập (CNN)

Mạng nơ-ron tích chập (CNN) là một kiến trúc mạng nơ-ron đặc biệt dành cho việc xử lý dữ liệu hình ảnh và giúp máy tính hiểu và phân tích hình ảnh một cách tự động. Nguyên tắc hoạt động của CNN dựa trên ba khái niệm chính: tích chập, tổng hợp và kích hoạt.Tích chập (Convolution): Lớp tích chập là lớp đầu tiên trong mạng CNN. Nó sử dụng các bộ lọc (hay còn gọi là kernel) để trượt qua ảnh đầu vào. Mỗi bộ lọc có thể nhận biết các đặc trưng cụ thể trong ảnh như cạnh, góc, hoặc hình dạng. Khi bộ lọc trượt qua ảnh, nó tạo ra các bản đồ đặc trưng (feature maps) bằng cách thực hiện phép tích chập giữa bộ lọc và vùng tương ứng trên ảnh. Các bản đồ đặc trưng này giúp mô hình nhận biết các đặc trưng quan trọng trong hình ảnh.
Tổng hợp (Pooling): Lớp tổng hợp thường đặt sau lớp tích chập. Nhiệm vụ của lớp này là giảm kích thước của các bản đồ đặc trưng bằng cách lấy giá trị lớn nhất hoặc trung bình từ các vùng nhỏ trên bản đồ đặc trưng. Việc này giúp giảm số lượng tham số và chi phí tính toán, đồng thời làm giảm nguy cơ overfitting.
Kích hoạt (Activation): Lớp kích hoạt áp dụng một hàm kích hoạt phi tuyến lên các giá trị trong các bản đồ đặc trưng. Phép kích hoạt này giúp mô hình học cách biểu diễn các đặc trưng phức tạp và tạo tính phi tuyến cho mạng.
Lớp kết nối đầy đủ (Fully Connected Layer): Sau khi thông qua các lớp tích chập, tổng hợp và kích hoạt, dữ liệu được đưa vào lớp kết nối đầy đủ để thực hiện các tác vụ như phân loại hoặc dự đoán. Trong lớp này, các nơ-ron kết nối với tất cả các nơ-ron trong lớp trước, giúp học cách tổ hợp các đặc trưng để đưa ra dự đoán cuối cùng.
Toàn bộ quá trình này, từ lớp tích chập cho đến lớp kết nối đầy đủ, là quá trình học tự động. Mạng nơ-ron tự điều chỉnh các trọng số của các lớp để tối ưu hóa hiệu suất cho nhiệm vụ cụ thể, chẳng hạn như phân loại ảnh.